Hatashe the Informal Mathematician to the all Mathematicians and Physicists belongs to the entire world. The Mathematics about Psychohistory, the term Psychohistory popularized by Isaac Asimov in his Foundation Series and actually the idea developed by United States Founding Father's team which was lead by George Washington. Psychohistory is a branch of science that could predict the general course of future flow. First I would like to give special thanks to three books and its authors; the Republic by Plato, Foundation by Asimov and Audacity by Obama. The three books were helpful to understand the Psychohistorical Literacy. I am still trying to give its Psychohistorical Mathematics shape. Calculus was established by Newton and Leibnitz and today it is enough mature but the Psychohistory is a new born mathematics, not reached to such stage yet that could predict the future. I will not discuss here the literacy pose of psychohistory because already I stated lot of literacy description in my previous book 'Prime Radiant device Obama: Maliatashe's Hypothesis and the Principle Mathematics of Applied Psychohistory.' So, directly I will point out here mathematical definitions and Psychohistorical Mathematics that one day will come when psychohistory will be reached to such stage that can able to predict the future.
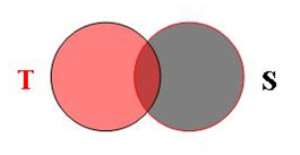
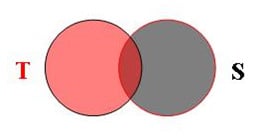
Let, T and S is the two Grids of Psychohistorical Revelation. Wherever 'T' stands for 'Time' and 'S' stands for 'Situation'. So, T is the Revelation of P, as well S is the Revelation of P, and T & S both is the coordinates of P. Now, if r the grid of T will be saturated to the b the grid of S, so r will be the feature equation of b. Wherever, r stands for Speaker Red and b stands for Obama Black. As well the same formula will applicable for Deviation Blue (bl), Notation Green (g), Projection Purple (p), White House (h), and Red Square Kremlin (rk).
So, the above equation's primary outline will be like þ(r) = X+Y+280
280 G.E. (G.E. Stands for George Era or Galactic Era, equivalent to 2012 C.E.)
As well þ(b), þ(bl), þ(g), þ(p), þ(h), þ(rk) will be same.
From Hatashe's 2nd Law which is Equation of Section 42R254,

S = 8.943518519, Where, 'S' is a Constant of Seldon plan or Seldon Constant.
If F= b, þ, bl, g, p, rk
So, þ(Ft) will be truth for any color equations of b, þ, bl, g, p, rk and for it's any values.
Dear Scientists, as per your response and valuable suggestions, I hope I will able to define a general course of past, present and future in the next paper, through mathematical equations along with the Maclaurin's Theorem. Maclaurin's Theorem states that the theorem giving conditions when a function, which is infinitely differentiable, may be represented in a neighborhood of the origin as an infinite series with nth term (1/n!) · ƒ(n)(0) · xn, where ƒ(n) denotes the nth derivative.
Maclaurin's theorem is a specific form of Taylor's theorem, or a Taylor's power series expansion, where c = 0 and is a series expansion of a function about zero. The basic form of Taylor's theorem is: n = 0 (f(n)(c)/n!)(x - c)n. When the appropriate substitutions are made Maclaurin's theorem is:
f (x) = f(0) + f'(0)x + f''(0)x2/2! + f(3)(0)x3/3! + ... f(n)(0)xn/n! +....
The Taylor's theorem provides a way of determining those values of x for which the Taylor series of a function f converges to f(x). I hope to get a response from you, Sir.




 Whoever participated in the plunder of the state must be held accountable – Jane...
Whoever participated in the plunder of the state must be held accountable – Jane...
 A vote for John and Jane is a vote to pull Ghana from the precipice of destructi...
A vote for John and Jane is a vote to pull Ghana from the precipice of destructi...
 I’ll repay your abiding confidence with loyalty, understanding and a devotion to...
I’ll repay your abiding confidence with loyalty, understanding and a devotion to...
 ‘I’ve learnt deeply useful lessons for the future' — Serwaa Amihere breaks silen...
‘I’ve learnt deeply useful lessons for the future' — Serwaa Amihere breaks silen...
 I’m sorry for the embarrassment – Serwaa Amihere apologises for leaked sex video
I’m sorry for the embarrassment – Serwaa Amihere apologises for leaked sex video
 Dumsor: Matthew Opoku Prempeh not in charge of Energy sector – Minority
Dumsor: Matthew Opoku Prempeh not in charge of Energy sector – Minority
 Adu Boahen’s murder: Police arrest house help who was in possession of deceased’...
Adu Boahen’s murder: Police arrest house help who was in possession of deceased’...
 Akufo-Addo nominates Felicia Attipoe as Tema West MCE
Akufo-Addo nominates Felicia Attipoe as Tema West MCE
 Election 2024: I can't have someone I defeated twice as my successor – Akufo-Add...
Election 2024: I can't have someone I defeated twice as my successor – Akufo-Add...
